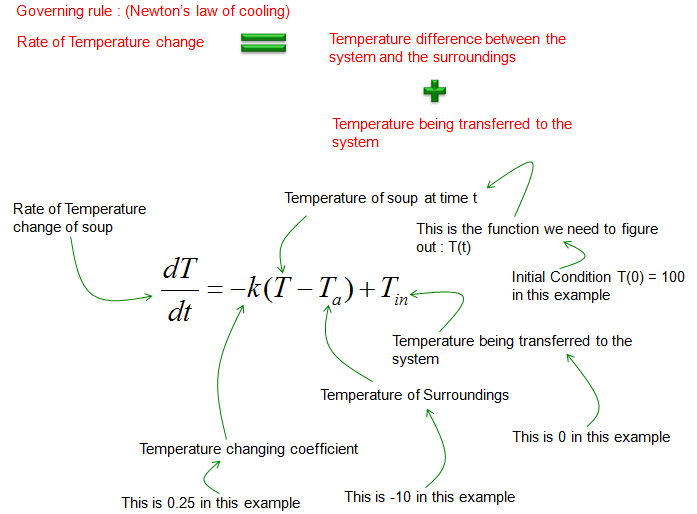
FlexPDEは有限要素法に基づく汎用性の高い偏微分方程式ソルバです。GB004 2次元熱伝導 という条件を適用することになります(ニュートンの冷却の法則)。 前の例では273度一定に保たれていたわけですが、今回の場合には周囲の冷却水の温度より150度(1) ニュートンの冷却の法則によれば, 銅球の温度が下がる速さは銅球と水の 温度差に比例する 比例定数をk としてY(t) の満たす微分方程式を立てよ 銅球の温度が下がる速さは¡Y0(t) (度=秒) 銅球と水の温度差はY(t)¡30 これらが比例するから Y0(t) = ¡k(Y(t)¡30)時間 における湯の室温との温度差を とすると、「Newtonの冷却の法則」 によれば (は正の定数) (A) より、微分方程式 が成り立つということになるのであるが、(A)式がどのようにして得られるか、について考察しようというのである。

5分でわかる ニュートンの冷却の法則 理系学生ライターがわかりやすく解説 Study Z ドラゴン桜と学ぶwebマガジン
ニュートン 冷却 微分方程式
ニュートン 冷却 微分方程式-熱伝導率が2層に分かれている場合、熱伝導方程式を貼り合わせることになりますが、その境界温度はニュートンの冷却の方式から、逃げる熱量をΔQを一定にしますから、αが24倍ある分、Ts – Ta が1/24になります。グラフでかくとこんな感じになります。というニュートンの運動方程式によって, 質点の運動(の軌道)がただ1 つに定まる これは, 3つの未知関数 x ( t ) ;y ( t ) ;z ( t )に対する連立上微分




数検1級1次問題 Hashtag Posts And Instagram Pictures And Videos Offerdos Com
℃とするとき、ニュートンの冷却 法則に基づきx (t )に関する微分方程式を導け。ただし、C T は定数とし、k を微分方程式の 比例定数とする。ただし、k>0 とする。 (2) 最初、コーヒーの温度は℃であり、10 分後の温度は52℃であった。このとき、 分後のニュートンの冷却の法則 周囲の温度が一定に保たれているとき,ある物体とその温度差は,温度差に比例する速 さで減少する. つまり,温度差が大きいほど早く冷え,温度差が小さくなるとゆっくり冷ニュートンの冷却法則についての質問ですが、 ニュートンの ニュートンの冷却の法則とは goo Wikipedia (ウィキペディア) ニュートンの冷却法則(その 1 Newton's Law of Cooling, Part 1
これは「ニュートンの冷却の法則」と呼ばれていますが、あくまで近似的に成り立つ式です。 微分方程式の解析解 ここでは微分方程式の解析解を求めてみます。 ニュートンの冷却の法則を表す微分方程式は微分方程式で数学モデルをつくる2 ニュートンの冷却法則 課題 お湯の中に浸された金属の塊を空気中に取り出すと、その温度はどのような時間変化をするか? 金属塊を取り出してからの時間 tと温度 Tの関係を予想して、そのグラフの概形を描きなさい。比例定数です。この微分方程式は,高等数学を使って解くことができます。 T – C = (T – T o)eLkt ただし,T o は t = 0 のときの物体の温度です。 この実験では,冷却する物体の温度変化を調べ,ニュートンが見出した数学的モデルを検証し ます。 必要な装置 CBL
第3回:エクセルで解こう!微分方程式 第4回:放射性炭素(C14)年代測定:アーサー王と円卓の騎士を題材として 第5回:a) 血中アルコール濃度と飲酒運転の事故発生率を題材として b) 冷却と加熱:ニュートンの冷却法則を題材としてうさぎでもわかる微分方程式 Part01 変数分離形(1階微分方程式 熱伝導方程式; 物体の冷える速度は、物体の温度と周囲の温度の温度差に比例する。 時刻 t における物体の温度を T 、周囲の温度を 、さらに比例定数を k>0 とすると、ニュートンの冷却法則は、次の微分方程式で表すことができる。



計算科学をはじめよう ニュートンの冷却法則 世界はフラクタル




5分でわかる ニュートンの冷却の法則 理系学生ライターがわかりやすく解説 ページ 2 3 Study Z ドラゴン桜と学ぶwebマガジン
温度センサーを例にとり、ニュートンの冷却 の法則について考える。周知のように、物体の 温度をµ、周囲の温度をµ0、そして時間をt で 表すと、ニュートンの冷却の法則は、 (1) dµ dt = ¡k(µ ¡µ0) (k > 0) という微分方程式で表される。簡単な微分方程ニュートンの冷却の法則 (ニュートンのれいきゃくのほうそく、 英 Newton's law of cooling )は、 液体 や 気体 などの 媒質 中におかれた高温の 固体 が媒質によって冷却される様子を表した 法則 であ*として温度の変化に注目してみると、次の偏微分方程式が成立する(熱伝導方 1/6 14 化学実験法II(吉村(洋))



表面張力の研究 改良版




微分方程式
冷却に関するニュートン(牛頓)の法則 「熱された物体とその周囲との間の温度差θは、温度差に比例する速度で減少する」 冷却に関するニュートンの法則 dθ/dt=-kθ いま t=0においてθ=θ 0 と仮定すれば この微分方程式の解は次のようになる。 θ冷却に関するニュートンの法則 dθ/dt=-kθ いま t=0においてθ=θ 0 と仮定すれば この微分方程式の解は次のようになる。 θ(t)=θ 0 e -kt 殺人事件の被害者の死体が、ある夜11時に発見された。 微分方程式 ニュートンの冷却の法則を表す微分方程式は で表されます。 ここで 変数 は時間、 はコーヒーの温度(時間の関数であることを明示したい場合は と書く) 定数 は周囲 (surroundings) の温度、 は冷却定数 です。 冷却定数 は 熱移動の機構




5分でわかる ニュートンの冷却の法則 理系学生ライターがわかりやすく解説 Study Z ドラゴン桜と学ぶwebマガジン



素人考えの数学論 微分方程式2 鹿児島alien 旧東京から鹿児島へ
(4)熱伝達(ニュートン冷却) − = − = k ∞ T x hT T x s ∂ ∂ 0 (3)断熱、対称 ∂ ∂ T x x = =0 0 (2)表面熱移動量(熱流束) − = = k T x q x w ∂ ∂ 0 (1)表面温度 Ts=const,Ts=g(x)orf(t)org(x) 物理学 ニュートンの冷却法則が導出できません。 熱電対の実験で、 「物体の冷却速度は周囲との間の温度差に比例し、 その比例定数をαとする」という仮定からニュートンの冷却の法則 「T=T2+(T1- 質問No 第1週目:熱伝導の物理的考察・数学的表現 こんにちは! ! ! 美里です。 今回の授業では、 ニュートンの冷却法則 によって出来た 連立微分方程式 を、 定数係数線形連立微分方程式 を用いて解いていく授業でした。 実際に例題を説明していきます。




ニュートンの冷却の法則 倭算数理研究所




微分方程式と数理モデル 遠藤 雅守 北林 照幸 共著 紀伊國屋書店ウェブストア オンライン書店 本 雑誌の通販 電子書籍ストア
ニュートン の冷却の法則を表す 微分方程式 は dT dt = − r(T − Ts) ⋯(∗) 冷却に関するニュートン(牛頓)の法則 「熱された物体とその周囲との間の温度差θは、温度差に比例する速度で減少する」 冷却に関するニュートンの法則 dθ/dt=-kθ いま t=0においてθ=θ 0 と仮定すれば 死亡推定時刻(微分方程式の応用) 午後11時30分に死体発見.そのときの体温は345 Cもう一つは,微分方程式の「解き方」以外の側面に光を当て,微分方程式を解かなくてもわかる洞察について,また一見まったく異なる二つの現象が共通の微分方程式で記述できるという面白さについて述べた. 53 加熱と冷却 531 ニュートンの冷却の偏微分が関係しない微分方程式を、『常微分方程式』と言います。 一変数関数の偏微分は常微分なので、常微分方程式は偏微分方程式の一 種とも言えます。ニュートン方程式が常微分方程式なので、力学では常 微分方程式を解くことがほとんどです。




これだけ 微分方程式の通販 古山 竜司 紙の本 Honto本の通販ストア



1zigen
1 1 回答 ニュートンの冷却法則について、学校から課題が出されました。 コーヒーの温度の下降速度は室温とコーヒーの温度の差に比例するとして微分方程式をたてろというものなのですが、考えるときコーヒ ニュートンの冷却法則について、学校から課題が出されました。 コーヒーの温度の下降速度は室温とコーヒーの温度の差に比例するとして微分方程式を14 モデル化:分離可能な方程式 例3 暖房の問題(ニュートンの冷却の法則) 就寝の2時間前に家の暖房を切る。この時刻を =0とする。 時刻 =0の時の温度𝑇=66度華氏 就寝する時𝑇=2には63度になっていた。 それから8時間後 =10の朝の温度を予想しなさい。ニュートンの冷却法則は次の微分方程式で表すことができます。 ΔT = k(T C) Δt Tは物体の温度、Cは室温、kは比例定数です。そして、ΔTは非常に短い時間のΔt間における物体の温度変化になります。Δtこそが微分の真骨頂で、限りなく0に近いことを示します。



2



計算科学をはじめよう ニュートンの冷却法則 世界はフラクタル
14 モデル化:分離可能な方程式 例3 暖房の問題(ニュートンの冷却の法則) モデル 𝑇 = 𝑇−𝑇𝐴= (𝑇−32) 時刻 =0の時の温度𝑇=66度 初期条件 𝑇 𝑇−32 = 𝑇−32= 一般解 𝑇 =32 𝑘𝑡 𝑇0=32 =66 =34空気と固体の温度差が大きいと、 急速に冷えていき、 温度差が小さくなると、 冷え方が緩やかになることを思い出して、 式にしてみます。 このようなときは、微分方程式になります。 dT/dt = (T0 T)α こんな感じです。単な微分方程式も扱っていた. 以下,本テーマの概要を述べると 前半は直線・平面上の点の運動,放物運動の公式,運動の法則 中盤は微分方程式を通して積分と物理量の関係 後半は2階線形微分方程式



うさぎでもわかる微分方程式 Part01 変数分離形 1階微分方程式 工業大学生ももやまのうさぎ塾



微分方程式の問題なんですがわからないので教えてください ニュートンの冷却 Yahoo 知恵袋
ニュートンの冷却の法則 は 熱 体の喪失は、体とその周囲の間の 温度 の差に正比例します。法則は、温度差が小さく、熱伝達メカニズムの性質が同じであるという条件を含めるようにしばしば認定されています。したがって、熱損失と温度差の間を仲介する 熱伝達係数 は一定であるというよくある常微分方程式の入門書で標準に扱われる, 材料が扱われています それら は, 変数分離型方程式, 1階線形方程式に対する定数変化法, 2階の定数係数線形微分方 程式,2変数の非線形連立方程式のなす力学系の停留点の標準形の理論などの基礎的な部 微分方程式について質問です。 Ay'By=sinx (A,Bは定数) の答えを教えていただきたいです。 写真のように答えを求めたのですが、 (C1,C2は任意定数) 見直しとして Ay'Byを求めると、 C1sinxとなり、微分方程式の右辺であるsinxになりません。




ねこ騙し数学




物理学2階の微分方程式 Youtube
ニュートンの冷却法則の数値解 では次にニュートンの冷却法則の数値解をオイラー法を使って求めてみます。前々回の記事で書きましたが、この法則を表す微分方程式と解析解は以下のとおりです。 (4) (5) 数値解を求めたい(4)式に (6)



1zigen
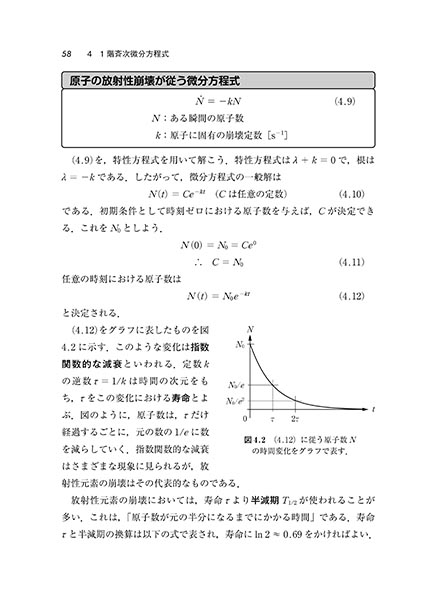



書籍紹介 微分方程式と数理モデル 遠藤雅守 北林照幸 共著 数学




計算科学をはじめよう ニュートンの冷却法則 世界はフラクタル




計算科学をはじめよう ニュートンの冷却法則 世界はフラクタル



2



1
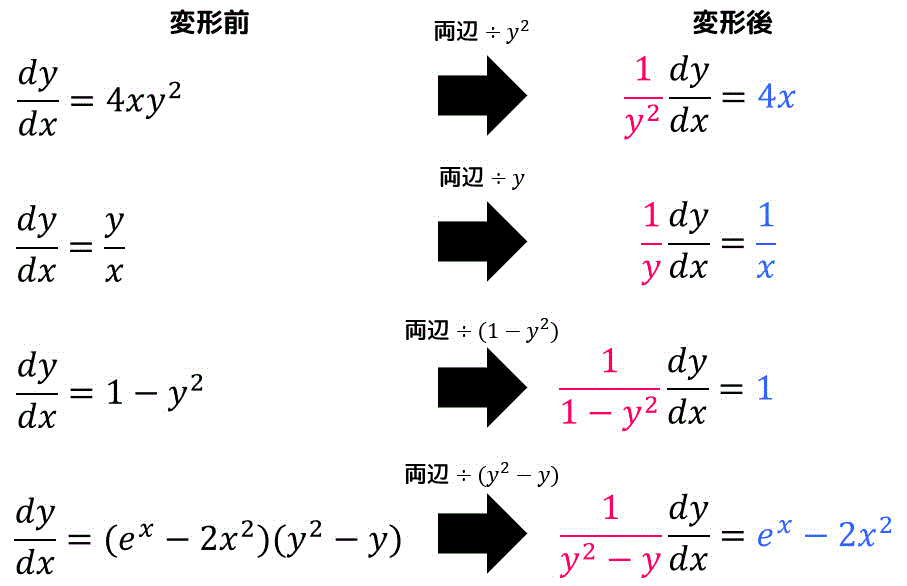



うさぎでもわかる微分方程式 Part01 変数分離形 1階微分方程式 工業大学生ももやまのうさぎ塾



冷却の法則




力学 1 スケールの話 2 いろいろな力 3 3次元空間内の運動の表現 動径ベクトル 4 速度ベクトル 加速度ベクトル Ppt Download




数値シミュレーション



ストゥルム リウビル型微分方程式の発見 熱方程式から 趣味の大学数学



1



2 6 コーヒーの冷却の問題 Cool 倭算数理研究所




微分方程式



ニュートンの冷却の法則




計算科学をはじめよう ニュートンの冷却法則 世界はフラクタル




ニュートンの冷却の法則 倭算数理研究所




ニュートンの冷却の法則
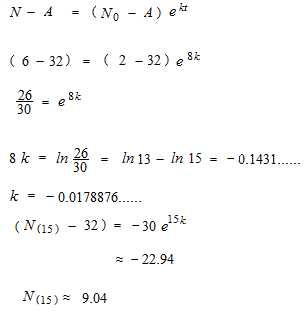



1 ニュートンの加熱の法則 Tokyomaths Com
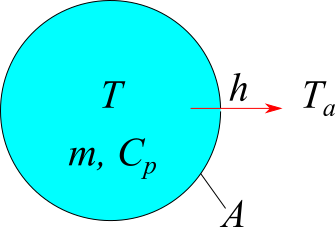



応用問題1 熱伝達による温度変化 科学技術計算講座1 9 科学技術計算ツール




計算科学をはじめよう ニュートンの冷却法則 世界はフラクタル




計算科学をはじめよう ニュートンの冷却法則 世界はフラクタル




Euler法で常微分方程式の数値解放をしましょう This Is Me Trying To Translate My By Siddik Acil Medium




数検1級1次問題 Hashtag Posts And Instagram Pictures And Videos Offerdos Com



松岡ヒロの実験報告 第3報 温度計の感温速度




5分でわかる ニュートンの冷却の法則 理系学生ライターがわかりやすく解説 ページ 2 3 Study Z ドラゴン桜と学ぶwebマガジン
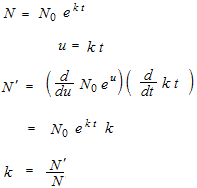



191 ニュートンの冷却の法則 Tokyomaths Com



2



ニュートンの冷却の法則 倭算数理研究所



ニュートン冷却の法則を使った時刻予想の問題 ある事件の被 Yahoo 知恵袋



ニュートン冷却法則を検証 科学アラカルト 実践 逆ポーランド電卓の実践ウェブ Rpn Hacks



ニュートン冷却法則を検証 科学アラカルト 実践 逆ポーランド電卓の実践ウェブ Rpn Hacks




Quenching And Boiling Protocol Translated To Japanese



対流熱伝達とは 制御工学の基礎あれこれ



計算科学をはじめよう ニュートンの冷却法則 世界はフラクタル



1
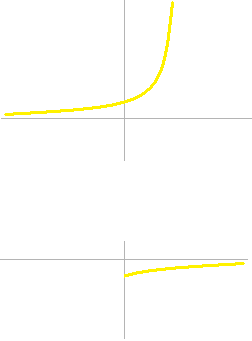



1 ニュートンの加熱の法則 Tokyomaths Com



1




ニュートンの冷却の法則 倭算数理研究所



I 1 1次元の熱伝導問題
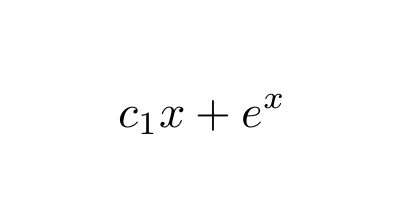



Euler法で常微分方程式の数値解放をしましょう This Is Me Trying To Translate My By Siddik Acil Medium



対流熱伝達とは 制御工学の基礎あれこれ



計算科学をはじめよう ニュートンの冷却法則 世界はフラクタル




ねこ騙し数学




1ylb23msr Hlnm
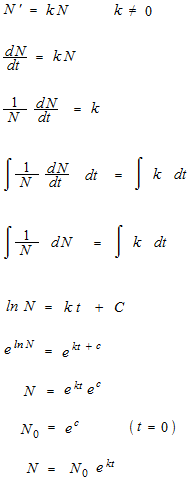



191 ニュートンの冷却の法則 Tokyomaths Com




楽天ブックス これだけ 微分方程式 古山竜司 本



三石 数学塾 コーヒーは何度か



Euler法で常微分方程式の数値解放をしましょう This Is Me Trying To Translate My By Siddik Acil Medium




微分方程式と数理モデル 現象をどのようにモデル化するかの通販 遠藤 雅守 北林 照幸 紙の本 Honto本の通販ストア




計算科学をはじめよう ニュートンの冷却法則 世界はフラクタル



2



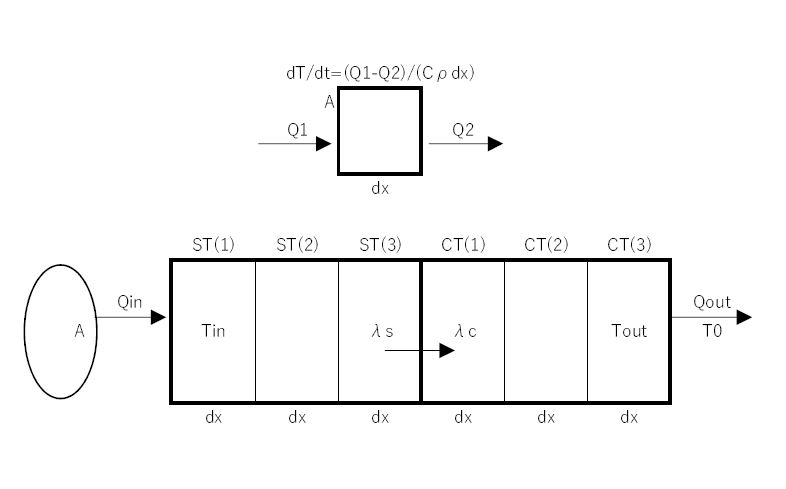
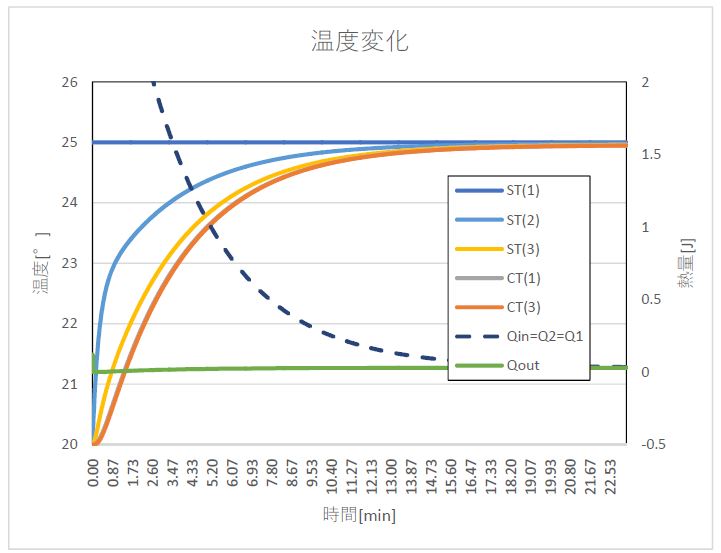
Gb004 2次元熱伝導 偏微分方程式ソルバ Flexpde ライトストーン




5分でわかる ニュートンの冷却の法則 理系学生ライターがわかりやすく解説 Study Z ドラゴン桜と学ぶwebマガジン



微分方程式の問題なんですがわからないので教えてください ニュートンの冷却 Yahoo 知恵袋



Pythonで簡単 死後経過時間推定 Qiita




ねこ騙し数学




ねこ騙し数学
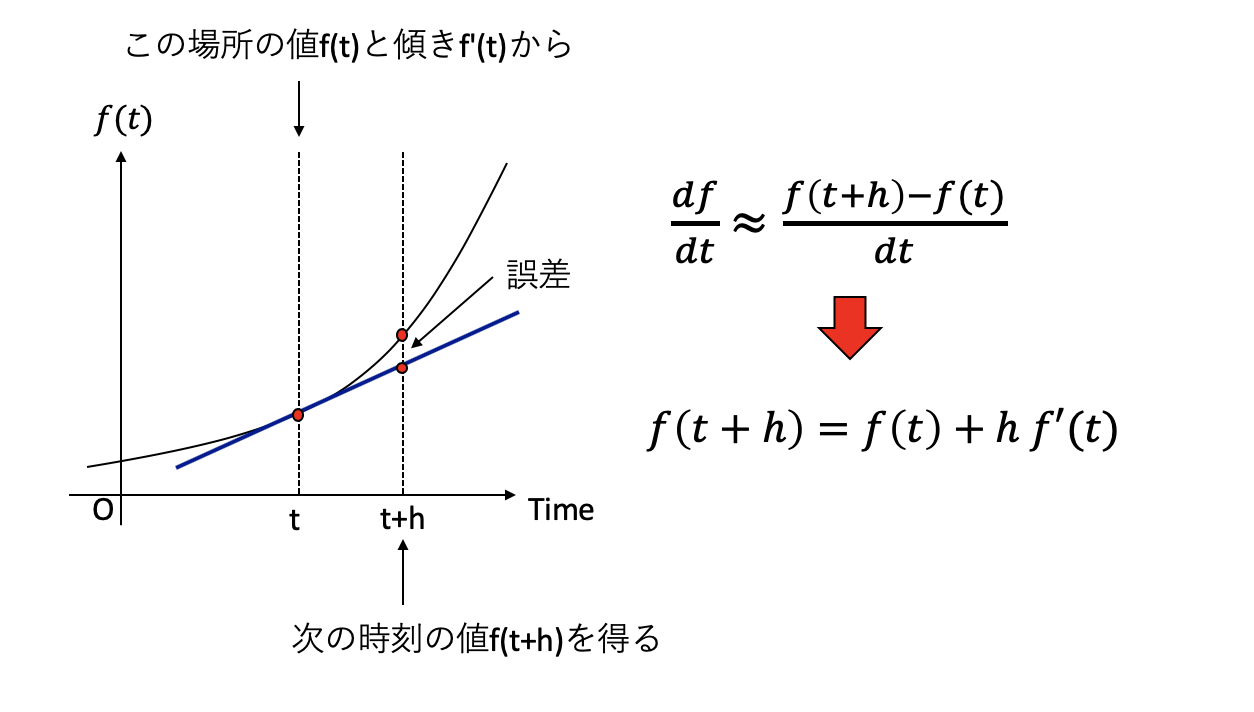



数値シミュレーション
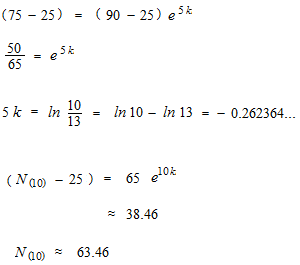



191 ニュートンの冷却の法則 Tokyomaths Com




5分でわかる ニュートンの冷却の法則 理系学生ライターがわかりやすく解説 Study Z ドラゴン桜と学ぶwebマガジン



2



2




5分でわかる ニュートンの冷却の法則 理系学生ライターがわかりやすく解説 Study Z ドラゴン桜と学ぶwebマガジン



2




Excelによる伝熱工学 対流伝熱




Entropy Protocol Translated To Japanese



2



2




Excelによる伝熱工学 対流伝熱
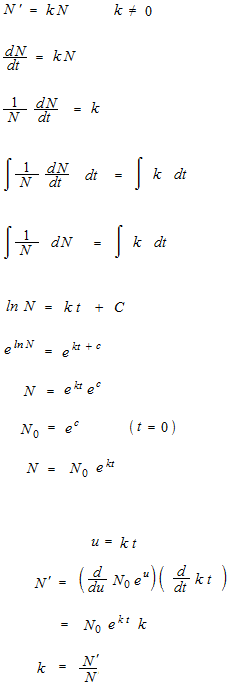



141 変数分離型 1階常微分方程式 バクテリア繁殖 Tokyomaths Com




微分方程式の応用 微分積分1より Youtube




書籍紹介 微分方程式と数理モデル 遠藤雅守 北林照幸 共著 数学



Akb48 ではなくてode45 Freematだと微分方程式が容易に解ける 無償ソフトで技術計算しよう シミュレーション基礎編 1 1 3 ページ Monoist




ニュートンの冷却の法則




Euler法で常微分方程式の数値解放をしましょう This Is Me Trying To Translate My By Siddik Acil Medium



ニュートンの冷却法則について カップに80 のコーヒーを入れた Yahoo 知恵袋




5分でわかる ニュートンの冷却の法則 理系学生ライターがわかりやすく解説 ページ 2 3 Study Z ドラゴン桜と学ぶwebマガジン




Euler法で常微分方程式の数値解放をしましょう This Is Me Trying To Translate My By Siddik Acil Medium



2
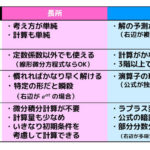



うさぎでもわかる微分方程式 Part01 変数分離形 1階微分方程式 工業大学生ももやまのうさぎ塾



ニュートンの冷却法則について カップに80 のコーヒーを入れた Yahoo 知恵袋




ニュートンの冷却の法則




指数関数的減衰 Wikipedia




微分方程式と数理モデル 遠藤 雅守 著 文 裳華房 版元ドットコム
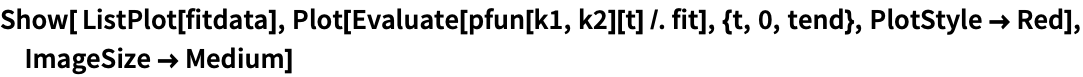



ニュートンの冷却の法則
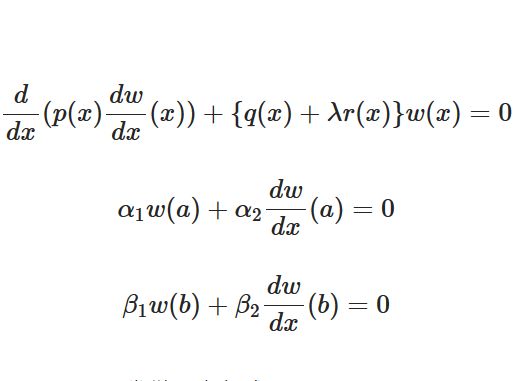



ストゥルム リウビル型微分方程式の発見 熱方程式から 趣味の大学数学
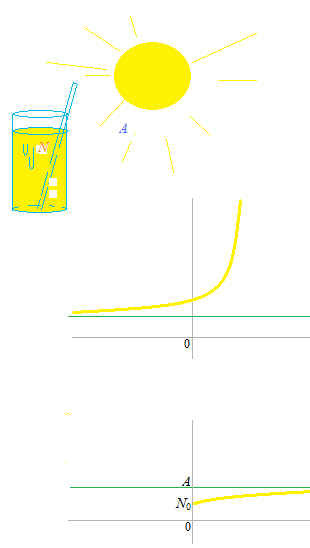



1 ニュートンの加熱の法則 Tokyomaths Com



0 件のコメント:
コメントを投稿